非球形行星与其宿主星（或月球）间的引力作用将导致其自转速度的不均匀变化，出现经向天平动现象，由此在其液核流体上生成一个Poincare力。由于对太阳系中行星而言，其对应的Poincare力一般均很小，所以对液核流体产生的影响并不显著。但若经向天平动能共振激发液核中流体的某个惯性波动，那么由此将产生较强的流体运动，研究其时空结构如何将变得十分有意义。 
    对于该问题，以前曾有过几个研究，认为当经向天平动频率若与流体的某个特征频率处于共振时，沿着流体转动轴方向，极区与中心的压强差变化较大，在极区会形成一个“尖峰”，由此人们认为经向天平动将导致共振流的产生。 
    我们采用渐进分析、线性数值分析和非线性数值模拟三种方法较深入全面地研究了该问题。假设旋转球形行星液核处于振幅为O(ε)量级的经向天平动状态下，结果表明，对于液核流体任何特征频率的运动，其振幅总是处于O(ε)量级，这意味着在经向天平动的液核中，流体运动不会出现共振现象。

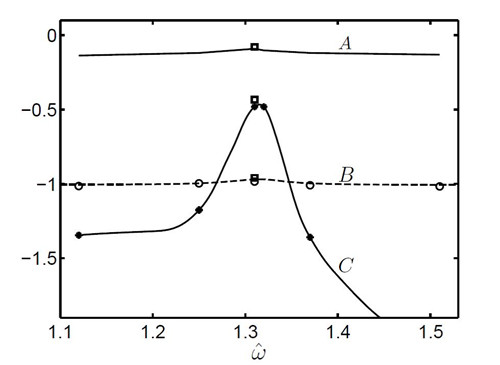
    尽管压强在极区出现“尖峰”，但在其它方向，比如赤道平面内，压强没有`显著变化。如图，对应Ekman数为10-4，ε是0.01；实线A表示由非线性数值模拟给出的在赤道面内压强随特征频率的变化（无尖峰），其上方块由分析解给出；虚线B表示由线性数值分析计算出的流体动能随特征频率的变化，其上方块是分析解给出的值，圆圈是非线性数值模拟的结果；实线C表示由非线性数值模拟给出的压强随特征频率的变化，其上方块是由分析解给出的值，星号表示在此处有非线性数值模拟给出具体的数值。 
    对经向天平动不会导致液核出现共振流，我们也从理论上给出具体解释。因此，经向天平动流将不会导致行星地球内部复杂的流体运动。